12: ANOVA: Comparison of k means 8/8/06

Review Questions

  1. Fill in the blank: The Mean Square Between (s2B) quantifies the variability of group means around the _________ mean.
  2. The Mean Square Within (s2w) quantifies the variability of observations values around __________ means.
  3. What symbol is used to denote the mean of population i? What symbol is used to denote the mean of sample i? 
  4. True or false?: The Mean Square Within is a pooled (weighted) average of group variances.
  5. What is the null hypothesis for one-way ANOVA? What is the alternative hypothesis? Is the alternative hypothesis one-sided, two-sided, or multi-sided?
  6. In an ANOVA comparing 4 groups of 8 people each, dfB = ____ and dfw = _____.
  7. We want to compare blood glucose levels in male and female taxi drivers. What is the outcome (dependent) variable in this analysis? What is the independent variable (factor)?
  8. What do you call the mean of all N individuals in a study?
  9. In an ANOVA, the factor being studied is __________________ [choose either quantitative or categorical] and the outcome (dependent) variable is  ___________________ [same choices].
  10. An ANOVA with two groups will produce the same P-value an equal variance __ test.
  11. What symbol is used to denote the grand mean? 
  12. What symbol is used to denote the sample mean of group i.
  13. The variance ___________  [choose within or between] groups can be thought of as background noise that interferes with detecting group differences.
  14. The variance within groups is equal to the sum of squares within groups divided by _____.
  15. Suppose Fstat = 3.26 with 3 and 14 degrees of freedom and F3,14,.95 = 3.34. Is P less than or greater than 0.05? Justify your response by drawing the F distribution and showing the Fstat on the horizontal axis of the curve. . 
  16. The variance between group means is equal to SSB divided by the _________.
  17. Vocabulary words: One-way ANOVA, grand mean, sum of squares within, sum of squares between, Mean square within, Mean square between, dfB,  dfW, F distribution, F statistic

Exercises

12.1 Weight gain and junk food (deermice.sav). An experiment randomly assigned lab mice to one of three groups. Group 1 received a standard diet, group 2 received a diet of junk food, and group 3 received a diet of health food. Weight gains (grams) after 5 weeks were:

Group 1 (standard diet):   11.8   12.0   10.7    9.1   12.1
Group 2 (junk food):       13.6   14.4   12.8   13.0   13.4
Group 3 (health food):      9.2    9.6    8.6    8.5    9.8

(A) Calculate the means and standard deviations for each group. How do they compare?
(B) Construct side-by-side boxplots of the data. Describe what you see. 
(C) The grand mean is 11.240; N = 15. Conduct an ANOVA. Show all hypothesis testing steps. Interpret your results.
(D) Optional: Download deermice.sav and replicate the analyses in SPSS (Analyze > Compare Means > One-way ANOVA).

12.2 Bronchial reactivity (bronch-react.sav; source unknown). Fifteen asthmatic were studied to assess the short-term effects of exposure to irritant gases. Group 1 was exposed to sulfur dioxide, group 2 was exposed to nitrous dioxide, and group 3 was exposed to pure oxygen. The response variable is  an index of bronchial reactivity. The grand mean for the bronchial reactivity scores is 10.253 (s = 8.651, N = 15). Bronchial reactivity scores for the individual participants are shown below. Explore the data with side-by-side boxplots. Then test the means for a difference with a one-way ANOVA procedure..

Group 1 (sulfur dioxide) :   20.8    5.1   30.1   24.4   13.8
Group 2 (nitrous dioxide):    7.5   11.9    3.1    4.7   10.3    2.2
Group 3 (oxygen)         :    9.3    2.1    2.4    6.1

12.3 Adaptation to maternal roles (mat-role.sav; Nurcombe et al, 1984; Howell, 1995, pp. 302 - 304). This study considers adaptation to maternal roles. Group 1 women had low birth-weight infants and received training about the special needs of their infants. Group 2 women had low birth-weight infants and received no special training. Group 3 women had full-term babies and received no special training (control group). The dependent variable is a score to survey questions in which high values indicate difficulty adapting to motherhood. Here is a listing of the data set. (Data may also be downloaded in the form of mat-role.sav by right-clicking the highlighted text).

Group 1 (n =29)

Group 2 (n = 27)

Group 3 (n = 37)

24

21

12

13

19

25

29

10

14

12

24

16

14

17

13

11

25

10

12

16

13

13

26

11

13

19

20

13

17

23

10

18

16

11

18

20

13

13

11

19

21

12

11

27

17

11

29

18

27

14

18

13

17

18

13

13

15

14

25

13

16

16

15

15

18

13

12

11

13

16

16

10

12

11

12

12

21

12

22

13

20

16

 

14

17

 

14

 

 

12

 

 

20

 

 

12

 

 

17

 

 

15

 

 

11

 

 

13

 

 

11

(A) Explore the data with side-by-side boxplots. Report the most salient findings from this exploration. What do you make of the outside values? 
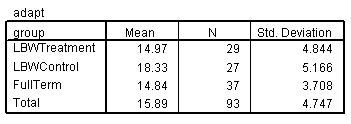
(B) Group summary statistics are shown below. Construct a one-way ANOVA table based on these summary statistics. Report the F statistic and P-value used to test H0: �1 = �2 = �3.


(C) In rejecting H0, are you concluding that all three groups differ? 

12.4 Fever reduction. Data on the effect of three fever-reducers are summarized in the table below. All patients were seen in the emergency room with a diagnosis of flu and all had a fever of 100.0oF to 100.9oF. Drugs were assigned randomly. Patients were telephoned 4 hours after administration of the drug to determine how much fever was subsequently reduced. Conduct an ANOVA.  Interpret your results. (Rosner, 2000, p. 569.) 

DRUG           n     MEAN REDUCTION     STD. DEV
Aspirin        5         1.50            0.61
Asp+ Acet.     5         0.36            0.58
Acetaminophen  5         0.08            0.77
OVERALL       15         0.65   

12.5 Sense of coherence (soc.sav; data are fictitious). Antonovsky (1985) proposed that a personal characteristic called "sense of coherence" (an amalgamation of a world view that see life as coherent, meaningful, and manageable, is hypothesized to be a determinant of health in coping with stress) fosters healthy living. Let us consider a fictitious survey that measured sense of coherence (SOC) in three groups. Group 1 is composed of concentration camp survivors, group 2 is composed of prison guards, and group 3 is composed of a random sample the population. Data are:

Group 1 (survivors):   131   167   113   134   178
Group 2 (guards)   :   105    52    71    56    85
Group 3 (controls) :   136   108   103    75   113

(A) Explore the data with side-by-side boxplots. 
(B) Calculate the mean and standard deviation of each group. 
(C) Test the means for a difference with a one-way ANOVA procedure. Show all hypothesis testing steps. Discuss the relevance of your finding..

12.6 Maternal smoking 1. Birth weights of infants (lbs.) in four groups are shown below (smoking-moms.sav; Rosner, 2000, p. 569). Group 1 mothers are nonsmokers. Group 2 are ex-smokers, Group 3 smoked approx. half-pack per day, and Group 4 smoked approx. one pack per day. 

Group 1 (non-smokers):   7.5   6.2   6.9   7.4   9.2   8.3
Group 2 (ex-smokers) :   5.8   7.3   8.2   7.1   7.8
Group 3 (half-pack)  :   5.9   6.2   5.8   4.7   8.3   6.2   
Group 4 (full-pack)  :   6.2   6.8   5.7   4.9   6.2   7.1   5.8   5.4

(A) Explore the data with a side-by-side boxplot. 
(B) Conduct an ANOVA and...
(C) ...discuss your findings.

12.7 Maternal smoking 2.  The variables and design of this study are similar to the study described in the prior exercise (exercise 12.6). Data have been changed and are stored in smok_bw.sav. Compare the groups with appropriate exploratory and inferential methods. Discuss your findings. 

Key to Odd Numbered Exercises                 Key to Even Numbered Exercises (may not be posted)