11: Variances and means (Key Odd)

Review Questions

1. Mean square error, mean square, residual error, variance within groups, "squared standard deviation"; population variance (parameter) = ²; sample variance (statistic) = s²
2. "Root mean square error"; population standard deviation = ; sample standard deviation = s
3. When the variable has a Normal distribution. 
4. Chebychev's inequality. 
5. Additional measures of spread: (1) inter-quartile range  (2) range. 
6. Boxplot visual clues for quantifying variability: hinge spread (i.e., IQR); "whiskers-spread"; range (which is often equal to the whisker's spread)
7. The sum of squares is the sum of the squared of deviation around the distribution's mean.
8. Recall that  s²  = SS / (n - 1). Therefore, SS = (n - 1)s²  
9. F-ratio test (and Levene's test)
10. Because pooling the variances suppress the non-uniformity of population variances.
11. False. The standard error is a measure of the mean's precision. 
12. df₁ = 11 - 1 = 10, df₂ = 10 - 1 = 9, and df = 10 + 9 = 19.
13. yes, and yes. 
14. t_16,.975 = 2.12
15. H₀:  ²₁ =  ²₂
16. Under the alternative hypothesis,  the variance in population 1 is larger than (or different from) the variance in population 2.
17. H₀: �₁ = �₂ versus H₁: �₁   �₂  
18. Population mean difference = �₁ - �₂; sample mean difference = ₁ - ₂ 
19. How to compare group variability (spreads) 
    (a) Descriptively (e.g., compare sample standard deviations or IQRs
    (b) Graphically (e.g., side-by-side boxplots) 
    (c) Testing (e.g., F ratio test; Levene's test)
20. How to compare group averages (central locations)
    (a) Descriptively (e.g., compare ₁ and ₂); 
    (b) Graphically (e.g., side-by-side stemplots, side-by-side boxplots, mean � SE plots) 
    (c) Testing (e.g., t test)
    (d) Confidence interval for �₁ -  �₂  
21.  It goes by various names including "Welch's modified t" and "the unequal variance t test". The general problem of comparing means from populations with unequal variances is called the Behrens-Fisher problem.

Exercises

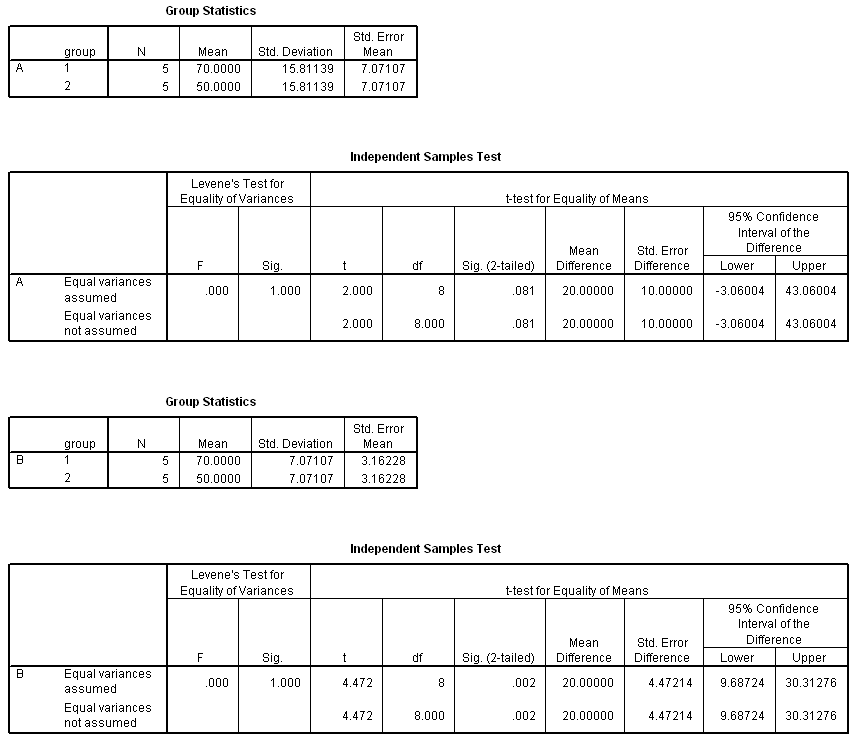
11.1  Comparing means depends on within group variability. ...we are confident the difference observed in Comparison B is real, while the observed difference in Comparison A might be due to chance fluctuation. Conduct t tests (for both comparisons) to confirm this suspicion. Calculations are shown below. Notice that even though Comparison A and Comparison B both compare a mean of 70 to a mean of 50, Comparison A derives P = 0.081, while Comparison B derives P = 0.002. Return to the stemplots in the exercise to see how this relates to the variability within groups.  

11.3 Linoleic acid and LDL cholesterol 

(A) Stemplot - The distribution for Group 1 is located toward the higher values (locations of medians underlined). Both distributions may sport modest positive skews, but there are  no apparent outliers. The ranges are visible.

 Group 1 | | Group 2
---------|-|---------
         |4|0
         |4|5
         |5|04  
     9888|5|6
    43100|6|04
       75|6|
        0|7|
         (�1) 

(B) Descriptive statistics

Group	n	mean  (mmol/m3)	s (mmol/m3)
1 (Cases, Rassias data)	12	6.192	0.3919
2 (Controls, fictitious)	7	5.271	0.8381

(C) F-ratio test of H₀: ₁² =  ₂² ; F_stat = 0.8381² / 0.3919²  = 4.573 w/ df₁ = 6 and df₂ = 11; 0.01 < P < 0.025. Significant: Yes!

(D) H₀: �₁ = �₂  vs. H₁: �₁  �₂  by Welch modified t test; SE_{mean dif}  = (.3919² / 12 + .8381² / 7) = 0.3364; t_stat = (6.192 - 5.271) / 0.3364 = 2.74; df by conservative hand-based method = 6 (df_Welch = 7.56); 0.025 < P < 0.05; the observed difference seems to be significant (reject H₀)

11.5 Body weight and pituitary adenoma. H₀:  ²₁ =  ²₂ ; F_stat = (21.4)² / (12.4)² = 2.98 with 11 and 4 degrees of freedom. P = 0.15. The evidence against H₀ is not significant.

11.7 Heart size and congestive heart failure.  

• Boxplots (below) show that group 1 has higher values on average and greater variability. The descriptive statistics (below boxplots) confirm the exploratory finding. Also notice that group 1 has a high outside value (evident on boxplot).
• The F ratio test of H₀:  ²₁ =  ²₂ derives F_stat = 19,415 / 2,218 = 8.75; Landmark on the table is F_10,9,.95 = 3.14; P < 0.05 (P = 0.0016). Variances differ significantly (reject H₀)
• Welch modified t test of H₀: �₁ = �₂ derives SE = 44.573; t_stat = 2.984, df = 12.452, P = 0.011. The means differ significantly.

11.9 Efficacy of echinacea (severity of symptoms.) 

• H₀: ₁² =  ₂² :F_stat= 1.09 with numerator df₁ = 369 and denominator df₂ = 336; P-value = 0.4264 Therefore, the variances to not differ significantly, and either t test can be used. We will use the unequal variance (Welsh) t test.
• H₀: �₁ = �₂  vs. H₀: �₁   �₂; use the unequal variances t_stat =  -0.5656 with df_W = 703.2 and P-value = 0.5719(calculated with SPSS v. 11). The conservative estimate is df_cons = 335. You can use the line that says " z"  (or use a z table) for t statistics with more than 100, so P > 0.40. This reveals no significant difference between the echinacea and the placebo group. 

Comment: The published source (Taylor et al., 2003) gives P  = 0.68 for a Cox regression for censored data. Our method is a simplification and uses rounded summary statistics ( reported in Table 2 of Taylor et al., 2003 ) but comes up with an equivalent answer. (I requested the original data from the author via email on 8/31/06, but have yet to receive a response.)

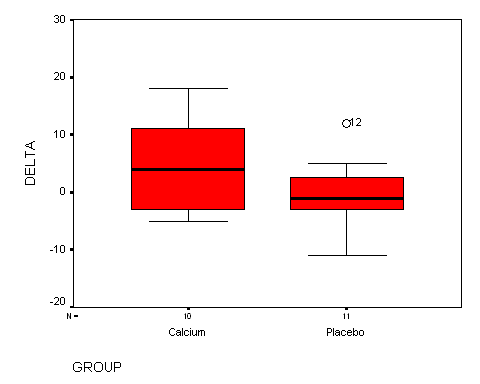
11.11 The effect of calcium supplementation on blood pressure. See the boxplot shown below. Notice that the calcium-supplemented group has a higher average and (perhaps?) more variation. Also notice the outside value in the placebo group.